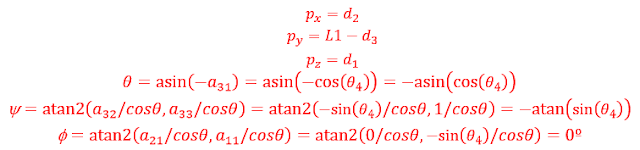Modelo cinemático directo e inverso de un robot portificado IRB 840A de ABB
1. Introducción:
En esta entrada se calculará el modelo cinemático directo e inverso del robot IRB
840A (Fig. 1) de la empresa ABB, además se calculará la posición y la orientación en coordenadas articulares para un punto dado en coordenadas de la base.
Fig. 1. Robot IRB 840A de ABB.
2. Parámetros Denavit-Hartenberg del robot
Siguiendo el procedimiento de Denavit-Hartenberg (D-H), colocaremos el sistema de coordenadas cartesianas de cada una de las articulaciones del robot (Fig. 2) y así encontrar la tabla de parámetros D-H.
Fig. 2. Sistema de coordenadas cartesianas de cada una de las articulaciones del robot (el sistema S4 está exactamente en el mismo punto que el S3)
A partir del sistema de coordenadas obtenemos la tabla de parámetros de Denavit-Hartenberg, como se muestra en la Tabla 1.
Articulación
|
θ
|
d
|
a
|
α
|
1
|
90º
|
d1
|
L1
|
90º
|
2
|
90º
|
d2
|
0
|
-90º
|
3
|
0
|
d3
|
0
|
0
|
4
|
q4
|
0
|
0
|
0
|
Tabla 1. Tabla de parámetros D-H.
3. Cinemática Directa.
Con la tabla de parámetros ya definida encontramos la cinemática directa del robot:
Aquí s representa la función seno y c la función coseno.
La función atan2(Y, X) calcula el arcotantegente de cuatro cuadrantes tan-1 de Y y X.
4. Cinemática Inversa.
A partir de la matriz de transformación homogénea global T y de las otras matrices de transformación A podemos encontrar la posición de la herramienta con respecto al origen en la base del robot.
Para encontrar q4 usamos el “desacoplo cinemático” ya que esta variable no modifica la posición del extremo del robot, solo su orientación y la matriz de orientación T ya es conocida.
Otra solución también puede ser q4 ± np, en donde n es un número
natural.
5. Posición y orientación en coordenadas de la base de un punto expresado en coordenadas articulares.
Para este ejemplo encontraremos la posición y orientación para el punto: [1, 1, 1, 120º], con L1 = 2.5 m.
d1 = 1, d2 = 1, d3 = 1, q4 = 120p/180.
La posición para el primer punto es: px = T(1,4) = 1, py = T(2,4) = 1.5, pz= T(3,4) = 1.
Extrayendo los ángulos de Euler (roll, pitch, yaw) de la matriz de orientación:
Podemos comprobar este último resultado si realizamos todas las rotaciones según Euler sobre el sistema fijo (Fig, 3).
Fig. 3. Rotaciones de Euler para la articulación q4.
El sistema fijo es O(XYZ) y el sistema móvil es A(OXYZ) y coinciden inicialmente. Los movimientos que se hacen son:
- Rotar el sistema A(OXYZ) un ángulo ψ de -90° alrededor del eje OX resultando el sistema A(OX'Y'Z') en rojo, a esta rotación se le denomina Alabeo (Roll).
- Rotar el sistema A(OX'Y'Z') un ángulo θ de 30°, alrededor del eje OY resultando el sistema B(OX''Y''Z'') en verde, a esta rotación se le denomina cabeceo (Pitch).
- Rotar el sistema B un ángulo ϕ de 180°, alrededor del eje OZ resultando el sistema C(OX'''Y'''Z''') en naranja, a esta rotación se le denomina guiñada (Yaw).
A la derecha, en la Fig. 3, se observa como las rotaciones de Euler giran a la articulación 4 los 120° pedidos en el marco de referencia de la herramienta.
6. Conclusiones.
El método de Denavit-Hartenberg es aplicable tanto a robots seriales homomorfos como a robots cartesianos, tal como el visto en este ejemplo, y nos da una herramienta para facilitar el cálculo de la cinemática directa e inversa de estos robots. También es necesario relacionar las posiciones articulares con el método de los ángulos de Euler, para definir la rotación de un cuerpo rígido, realizando tres rotaciones sucesivas alrededor de un sistema de coordenadas fijo.